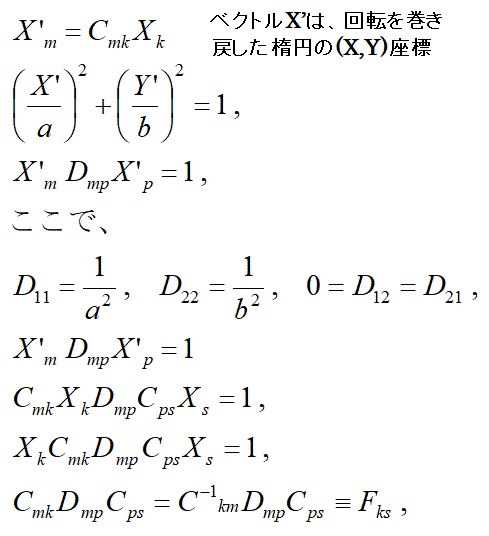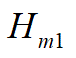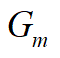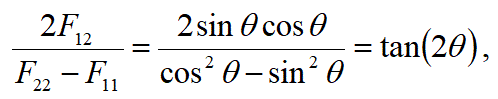《目次》行列演算からベクトル解析まで
内部リンク:
▷行列式
▷行基本変形や余因子展開の計算方法
【行列式】
ケイリー・ハミルトンの定理の数学的意味を理解するためには、先ず、「行列式」の意味を知る必要があります。
行列式は、ベクトルが張る図形の面積や体積を計算するものです(前のページで説明)。
「行列式」は、行の数と列の数が同じ正方行列の場合に計算できるものです。
(2行2列の行列の行列式)
2行2列の行列の行列式は、
その行列の要素が構成する2つの縦ベクトルが作る平行四辺形の面積をあらわすという意味を持ちます。
2行2列の行列Ampの行列式は、
エディントンの行列式の計算記号εmpを使って、アインシュタインの縮約記法であらわして、
εmpAm1Ap2
で計算します。
この計算に利用する行列
εmp
は、m≠pの場合の、
ε12=1,
ε21=-1
であり、それ以外の、m=pとなる、
εmp=ε11=ε22=0
です。
行列式
εmpAm1Ap2
は、ベクトル(A11,A21)とベクトル(A12,A22)との作る平行四辺形の面積をあらわすという意味を持ちます。
行列式を具体的に計算すると、
εmpAm1Ap2=A11A22-A21A12
です。
なお、行列式の計算方法は、行と列を入れ替えても変わらない、行と列に関して対称な式になっています。
すなわち、行列式は、以下の式でも計算できます。
εmpA1mA2p
以下で、行列式がベクトルの作る平行四辺形の面積を計算するものであることを説明します。
(一言で言うと、行列式の計算式を見ると、
1列目のベクトルに垂直で長さが同じベクトルと、2列目のベクトルとの内積の計算であることがわかります。
その計算は、1列目のベクトルを底辺として2列目のベクトルを斜辺とする平行四辺形の面積を計算するものです。
これで証明ができてしまいましたが、以下の証明も面白いので読んでください。)
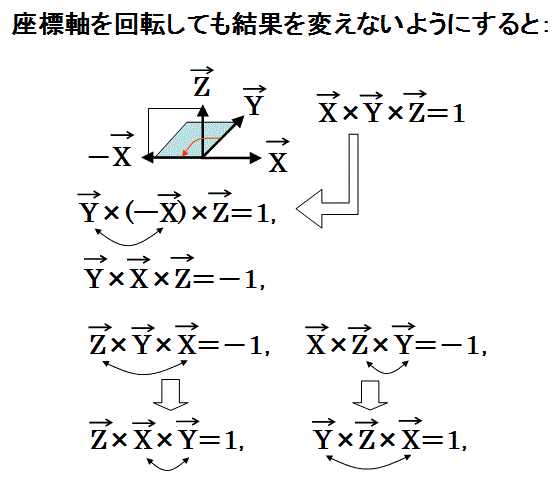
以下のように、座標が回転しても結果が変わらないように面積の計算規則を定める点がポイントです。
X座標軸を回転させてY座標軸に重ねると、Y座標軸はX座標軸の負の方向を向いて重なる。そのため、X成分にY成分を掛け算した結果を正にした場合、このように座標を回転させても面積が変わらないようにするには、必然的に、Y成分にX成分を掛け算した結果を負にしなければならない。それで、計算規則が、行列式の計算規則に定まってしまうのです。
(平行四辺形の面積を1つ目のベクトルに垂直なベクトルと2つ目のベクトルの内積であらわす)
三角形の面積Sは、以下の様に、ベクトルAに垂直なベクトルAvとベクトルBの内積であらわすことができます。
(式1’が平行四辺形の面積2Sの公式)
こうして得た式1’は、先に計算した行列式による面積の計算式1aと同じ式になりました。
すなわち、2行2列の行列式は、ベクトルAに垂直なベクトルAvとベクトルBの内積であらわすことができます。
(3行3列の行列式)
3行3列の行列の行列式は、その行列の要素が構成する3つの縦ベクトルが作る斜方体の体積をあらわすという意味を持ちます。
3行3列の行列Ampの行列式は、
エディントンの行列式の計算記号εmprを使って、アインシュタインの縮約記法であらわして、
εmprAm1Ap2Ar3
で計算します。
この計算に利用する行列(正しくは、擬テンソルと呼ばれる)
εmpr
は、m≠p、m≠r、p≠rの場合の、
ε123=ε231=ε312=1
ε213=ε321=ε132=-1
であり、それ以外の
εmpr=0
です。
行列式
εmprAm1Ap2Ar3
は、ベクトル(A11,A21,A31)とベクトル(A12,A22,A32)とベクトル(A13,A23,A33)との作る斜方体の体積をあらわすという意味を持ちます。
行列式を具体的に計算すると、
εmprAm1Ap2Ar3
=A11A22A33
+A21A32A13
+A31A12A23
-A21A12A33
-A31A22A13
-A11A32A23
です。
この行列式が斜方体の体積をあらわすので、3つの3次元ベクトルの先端と原点とを頂点とする三角錐の体積は、その3つの3次元ベクトルを3つの列ベクトルとする行列式の値を6分の1にした値になります。
このように、行列式は、行列を構成するベクトルが作る面積や体積をあらわします。
(n行n列の行列式)
ε(p1)(p2)(p3)・・・(pn){A(p1)1A(p2)2A(p3)3・・・A(pn)n}
で計算します。
ここで用いた添え字がn個の行列(正式には、添え字2つのものを行列と呼び、添え字3つ以上のものはテンソルと呼ばれる)
ε(p1)(p2)(p3)・・・(pn)は、以下の値を持ちます。
ε(1)(2)(3)・・・(n)=1
この添え字の位置を交換すると(-1)倍になる。例えば、1と2を交換すると、
ε(2)(1)(3)・・・(n)=-1
これらの添え字の位置を交換した要素以外は全て0です。例えば、
ε(1)(1)(3)・・・(n)=0
【行列式は行と列を入れ替えても結果が同じ】
行列式は、計算の元になる行列の行と列に関して対称な計算式です。そのため、行と列を入れ替えた行列でも行列式は同じ値になります。
【行列式が0になる行列の性質】
行列を列ベクトルに分割したとき、その列ベクトルが独立でなく、1つの列べクトルが他の列ベクトル(重みつき和)であらわせる場合は、行列式が0になります。
(2行2列の行列の場合)
例えば、2行2列の行列の場合は、行列式が0になる場合は、行列の2つの列ベクトルが、平行な2つのベクトルの場合です。
この平行な2つのベクトルで構成する平行四辺形の面積は0です。
行列式はその面積をあらわすものなので、その行列式は0になります。
(3行3列の行列の場合)
3行3列の行列の場合は、行列式が0になる場合は、行列を構成する3つのベクトルが、同一平面上にある場合です。
その3つのベクトルで構成される斜方体は、その平面上の高さが0であるので、体積が0です。
行列式はその体積をあらわすものなので、その行列式は0になります。
行列式は、そのうちの2つの行が同じ行ベクトルであると、行列式が0になります。2つの列が同じ列ベクトルの場合も0になります。
また、行列式が0になる行列は、あるベクトルを0ベクトルに変換する性質があります。後に説明する内容ですが、そのベクトルは、その行列の、値が0の固有値に対する固有ベクトルです。
そして、その固有ベクトルには、次のページで説明する余因子行列の列ベクトルが比例します。
なお、以下の行列式の積の計算は間違えやすい。
《行基本変形や余因子展開の計算方法》
【問1】
以下の行列式を計算せよ。
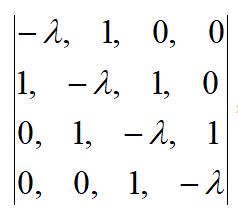
【解1】
余因子展開法で3行3列の行列式(2つ)の和にする。
その、各3行3列の行列式は、 サラスの方法で簡単に求められる。

(解答おわり)
【解2】
行列式の中の1行又は1列の中で、以下の式で赤〇で囲った1成分以外の他の成分が全て0になるようにうまく変形しつつ、1成分だけの余因子展開法を2段階に用いて解く。

上式の計算では、初めに、4行4列の行列式の中で、1列目に2列目のλ倍を加えることで、1行目の行の中を、赤〇で囲った1つの成分以外の全ての成分を0にする処理から計算を始めた。次に、その1行目の行に1成分だけの余因子展開法を用いた。
(解答おわり)
【問2】
以下の行列式を計算せよ。

【解答】
その行列式の中の3列目で、以下の式で赤〇で囲った1成分以外の他の成分が全て0になるようにうまく変形しつつ、1成分だけの余因子展開法を用いて解く。
先ず、2行目の3倍を1行目に足す。2行目を3行目に足す。
次に、2行目のλ倍を3行目に足す。

(解答おわり)
【問3】
以下の行列式を計算せよ。

【解答】
行に他の行のf倍を足す計算を繰り返す。
先ず、4行目の-(X+2)倍を1行目に足す。
4行目を2行目に足す。
4行目の-2倍を3行目に足す。

ここで、
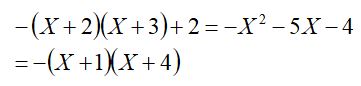
余因子展開法で
(-1)掛ける3行3列の行列式:

1行目に2行目の2倍を足す。

ここで、

余因子展開法で
(X+1)掛ける2行2列の行列式:

2行目の(-1)倍を1行目に足す。

ここで、

余因子展開法で

掛ける1行1列:
よって、行列式=
(解答おわり)
【問4】
以下の行列を行基本変形によって簡約化して、逆行列を計算せよ。

【解答】
行に他の行の整数倍を足す計算を繰り返す。
(1)ある行を整数倍して他の行に加える処理により、行列の成分がなるべく小さい数になるように変えていく。
(2)行の成分の最大公約数で行を割り算する。
(3)ある行の成分の大きさが大きい場合は、他の行を引き算することで成分を(0にしなくても良いから)小さくする。
先ず、以下の行列を作成する。

2行目から3行目を引く。
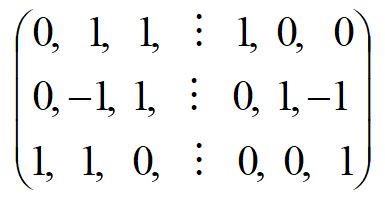
2行目に1行目を足す。

3行目、1行目、2行目の順に行を並び変える。

1行目と2行目を2倍にして、簡約化係数を2倍に揃える。

2行目から3行目を引く。

1行目から2行目を引く。

これで、以下の逆行列が求められた。

この逆行列を元の行列に掛け算して単位行列になることを確認する。

(解答おわり)
【問5】
以下の複素数成分を持つ行列を行基本変形によって簡約化して、簡約行列を計算せよ。
[4-6i][6][2]
[-2][1-6i][6]
[6][-2][4-6i],
【解答】
行に他の行の整数倍を足す計算を繰り返す。
(1)ある行を整数倍して他の行に加える処理により、行列の成分がなるべく小さい数になるように変えていく。
(2)行の成分の最大公約数で行を割り算する。
(3)ある行の成分の大きさが大きい場合は、他の行を引き算することで成分を(0にしなくても良いから)小さくする。
[4-6i][6][2]
[-2][1-6i][6]
[6][-2][4-6i],
1行目を2で割る。
3行目を2で割る。
[2-3i][3][1]
[-2][1-6i][6]
[3][-1][2-3i],
1行目に2行目を足す。
3行目に2行目を足す。
[-3i][4-6i][7]
[-2][1-6i][6]
[1][-6i][8-3i],
1行目に3行目の3i倍を足す。
2行目に3行目の2倍を足す。
[0][22-6i][16+24i]
[0][1-18i][22-6i]
[1][-6i][8-3i],
1行目を2で割る。
[0][11-3i][8+12i]
[0][1-18i][22-6i]
[1][-6i][8-3i],
1行目をi倍する。
[0][3+11i][-12+8i]
[0][1-18i][22-6i]
[1][-6i][8-3i],
1行目を2行目に足して2行目の成分の大きさを小さめにする。
[0][3+11i][-12+8i]
[0][4-7i][10+2i]
[1][-6i][8-3i],
2行目を1行目に足して1行目の成分の大きさを小さめにする。
[0][7+4i][-2+10i]
[0][4-7i][10+2i]
[1][-6i][8-3i],
1行目から2行目のi倍を引く。
[0][0][0]
[0][4-7i][10+2i]
[1][-6i][8-3i],
2行目を(4+7i)倍する。
[0][0][0]
[0][65][26+78i]
[1][-6i][8-3i],
2行目を13で割る。
[0][0][0]
[0][5][2+6i]
[1][-6i][8-3i],
次の計算の準備のために、3行目を5倍にする。
[0][0][0]
[0][5][2+6i]
[5][-30i][40-15i],
3行目に2行目の6i倍を足す。
[0][0][0]
[0][5][2+6i]
[5][0][4-3i],
(簡約化処理おわり)
なお、この行列を以下の行列に変換する。
[1][0][(4-3i)/5]
[0][1][(2+6i)/5]
[0][0][0],
(変形おわり)
この行列の一番右辺の列の列ベクトルの一番下の係数0を(-1)に変えて作った列ベクトルは、この行列によって0ベクトルに変換される。


リンク:
追加講:三角形の面積と行列式
高校数学の目次